Eigenvectors and Eigenvalues Tutorial Sheet, Sheet #4B
Learning targets
- Understand and produce visual representations of eigenvectors and eigenvalues
- Find the eigenvectors and eigenvalues for 2 x 2 and 3 x 3 matrices
Recap definitions
- Eigenvector: a vector which when operated on by a given operator gives a scalar multiple of itself.
- Eigenvalue: any number such that a given matrix minus that number times the identity matrix has zero determinant.
Additional Resources
Tutorials
- Linear Algebra Playlist : The same playlist as mentioned last week.
Software
- Eigen-calculator and Visualisation : Shows the eigs on a graph and calculates them for you - get an idea of where things move!
- Matlab Documentation : Information on eigenvectors and values on Matlab. Getting familiar with matlab will be a great advantage.
Problem sheet
Skill Building Questions
Problem 1.
Find the eigenvalues and the associated eigenvectors for the transformations represented in the following figures. (Note: The red vector shown is the result of transforming the blue vector. Be careful with the difference between the two arrowheads )
(a)
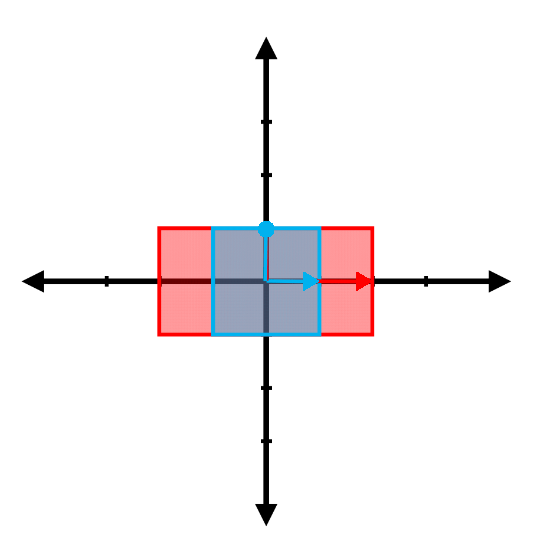
(b)

(c)
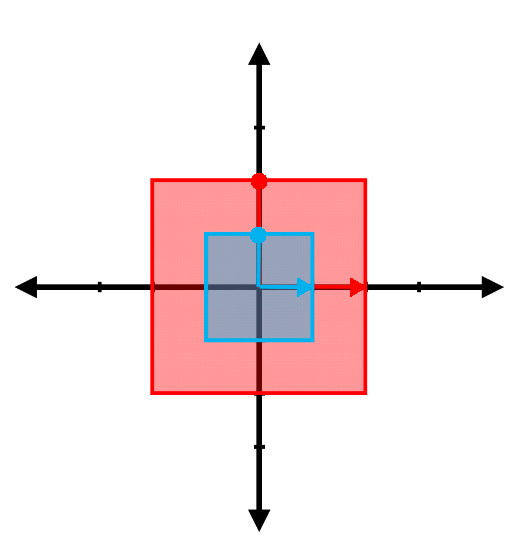
(d)
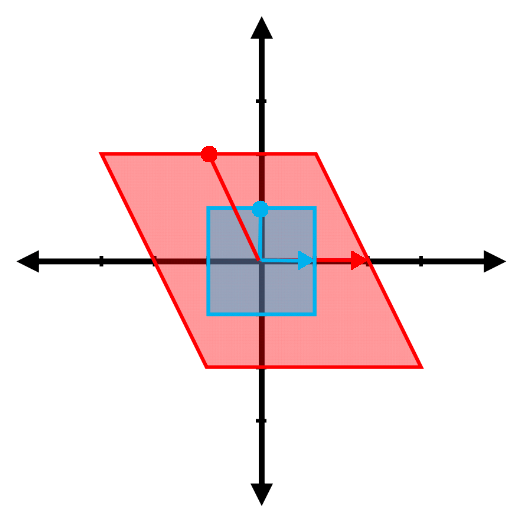
(e)
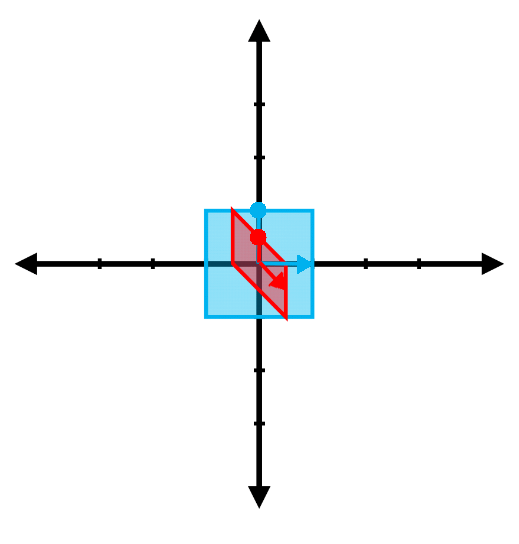
(f)
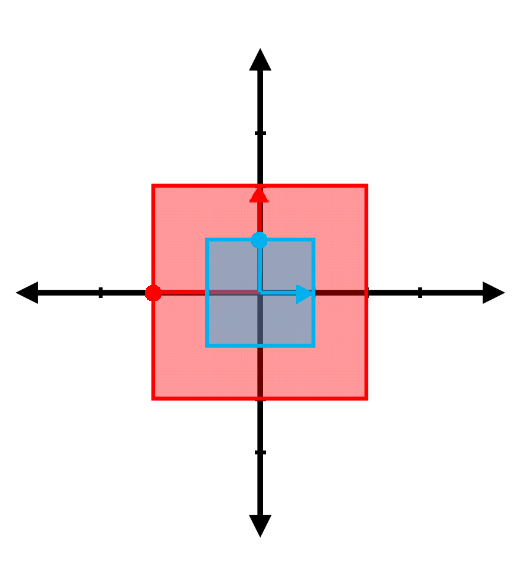
(g)
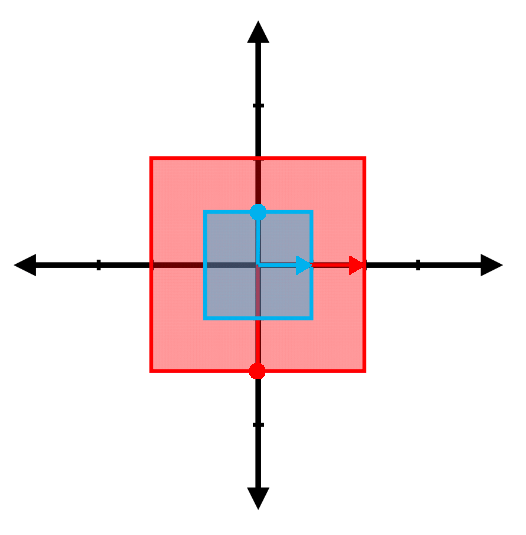
Problem 2.
Find the eigenvalues and the associated eigenvectors of the matrices:
A quick trick for finding the eigenvalues of a 2x2 matrix just by looking at it. This is a good way for double checking your answer. Remember what you learned last week with Matlab - it’ll make your life a lot easier…
(a) $\begin{pmatrix}1&3\\ 2&2\end{pmatrix}$
For $\boxed{\lambda_1 = 4, \begin{pmatrix}1,1\end{pmatrix}},$
For $\boxed{\lambda_2 = -1, \begin{pmatrix}-3,2\end{pmatrix}}.$
(b) $\begin{pmatrix}1&3&1\\ 0&5&0\\ 1&3&0\end{pmatrix}$
For $\lambda_1 = 5$ $\Rightarrow{}\quad \begin{pmatrix}-4&3&1\\\ 0&0&0\\\ 1&3&-5\end{pmatrix} \begin{pmatrix}x_1\\\ x_2\\\ x_3\end{pmatrix} = \begin{pmatrix}0\\\ 0\\\ 0\end{pmatrix} \Rightarrow{}\quad \begin{cases} \begin{aligned} -4x_1 +3x_2 +x_3 =& 0\\\ 0x_1 +0x_2 +0x_3 =& 0\\\ x_1 +3x_2 -5x_3 =& 0 \end{aligned} \end{cases}\\\ \Rightarrow{}\quad \begin{cases} x_1 = \frac{6x_3}{5}\\\ x_2 = \frac{19x_3}{15} \end{cases} \quad\Rightarrow{}\quad \text{ in parametric form } x_1=\frac{6t}{5},\quad x_2=\frac{19t}{15},\quad x_3=t \text{ for any } t \in R\\\ \Rightarrow{}\quad \text{ if } t=15, \text{ eigenvector of } \lambda_1:\quad (18,19,15)$
For $\lambda_2 = \frac{1+\sqrt{5}}{2}$ $\Rightarrow{}\quad \begin{pmatrix} 1 - \frac{1+\sqrt{5}}{2} & 3 & 1\\\ 0 & 5 - \frac{1+\sqrt{5}}{2} & 0 \\\ 1 & 3 & - \frac{1+\sqrt{5}}{2}\end{pmatrix} \begin{pmatrix}x_1\\\ x_2\\\ x_3\end{pmatrix} = \begin{pmatrix}0\\\ 0\\\ 0\end{pmatrix} \Rightarrow{}\quad \begin{cases} \begin{aligned} \bigg(1 - \frac{1+\sqrt{5}}{2}\bigg)x_1 + 3x_2 + x_3 =& 0\\\ \bigg(5 - \frac{1+\sqrt{5}}{2}\bigg)x_2 =& 0\\\ x_1 + 3x_2 -\bigg(\frac{1+\sqrt{5}}{2}\bigg)x_3 =& 0 \end{aligned} \end{cases}\\\ \Rightarrow{}\quad \begin{cases} x_2 = 0\\\ x_1 = \bigg(\frac{1+\sqrt{5}}{2}\bigg)x_3 \end{cases} \quad\Rightarrow{}\quad \text{ in parametric form } x_1=\bigg(\frac{1+\sqrt{5}}{2}\bigg)t,\quad x_2=0,\quad x_3=t \text{ for any } t \in R \\\ \Rightarrow{}\quad \text{ if } t=1, \text{ eigenvector of }\lambda_2:\quad \big(\frac{1+\sqrt{5}}{2}, 0, 1\big)$
For $\lambda_3 = \frac{1-\sqrt{5}}{2}$ $\Rightarrow{}\quad \begin{pmatrix}1-\frac{1-\sqrt{5}}{2} & 3 & 1 \\\ 0 & 5-\frac{1-\sqrt{5}}{2} & 0 \\\ 1 & 3 & -\frac{1-\sqrt{5}}{2}\end{pmatrix} \begin{pmatrix}x_1\\\ x_2\\\ x_3\end{pmatrix} = \begin{pmatrix}0\\\ 0\\\ 0\end{pmatrix}\\\ \Rightarrow{}\quad \begin{cases} x_2 = 0\\\ x_1 = \bigg(\frac{1-\sqrt{5}}{2}\bigg)x_3 \end{cases} \quad\Rightarrow{}\quad \text{ in parametric form } x_1=\bigg(\frac{1-\sqrt{5}}{2}\bigg)t,\quad x_2=0,\quad x_3=t \text{ for any } t \in R$ $\Rightarrow{}\quad \text{ if } t=1, \text{ eigenvector of } \lambda_3:\quad \big(\frac{1-\sqrt{5}}{2}, 0, 1\big)$
To summarise:
$\boxed{\text{For } \lambda_1 = 5, \begin{pmatrix}18\\\ 19\\\ 15\end{pmatrix} \\\ \text{For } \lambda_2 = \frac{1+\sqrt{5}}{2}, \begin{pmatrix}\frac{1+\sqrt{5}}{2}\\\ 0\\\ 1\end{pmatrix} \\\ \text{For } \lambda_3 = \frac{1-\sqrt{5}}{2}, \begin{pmatrix}\frac{1-\sqrt{5}}{2}\\\ 0\\1\end{pmatrix}}$
(c) $\begin{pmatrix}3&1&1\\ 2&4&2\\ 1&1&3\end{pmatrix}$
$\Rightarrow{}\quad$ eigenvalues: $\lambda_1=2,\quad \lambda_2=2,\quad \lambda_2=6$
For $\lambda_1 = 2$ and $\lambda_2 = 2$ $\Rightarrow{}\quad \begin{pmatrix}1&1&1\\\ 2&2&2\\\ 1&1&1\end{pmatrix}\begin{pmatrix}x_1\\\ x_2\\\ x_3\end{pmatrix} = \begin{pmatrix}0\\\ 0\\\ 0\end{pmatrix} \quad\Rightarrow{}\quad x_1 + x_2 + x_3 = 0 \quad\Rightarrow{}\quad x_1 = -x_2 -x_3$ $\Rightarrow{}\quad$ in parametric form $x_1=-t-u,\quad x_2=t,\quad x_3=u$ for any $t,u \in R$ $\Rightarrow{}\quad$ if $t=0$ and $u=1$, eigenvector of $\lambda_1: (-1,0,1)$ $\Rightarrow{}\quad$ if $t=1$ and $u=0$, eigenvector of $\lambda_2: (-1,1,0)$
For $\lambda_3 = 6$ $\Rightarrow{}\quad \begin{pmatrix}-3&1&1\\\ 2&-2&2\\\ 1&1&3\end{pmatrix}\begin{pmatrix}x_1\\\ x_2\\\ x_3\end{pmatrix} = \begin{pmatrix}0\\\ 0\\\ 0\end{pmatrix} \quad\Rightarrow{}\quad \begin{cases} -3x_1 + x_2 + x_3 = 0\\\ 2(x_1 - x_2 + x_3) =0\\\ x_1 + x_2 - 3x_3 =0 \end{cases}\quad\Rightarrow{}\quad \begin{cases} x_1 = x_3\\ x_2 = 2x_3 \end{cases}$ $\Rightarrow{}\quad$ in parametric form $x_1=t,\quad x_2=2t,\quad x_3=t$ for any $t \in R$ $\Rightarrow{}\quad$ if $t=1$, eigenvector of $\lambda_3: (1,2,1)$
To summarise:
$\boxed{\text{For } \lambda_1 = 2 \text{ and } \lambda_2 = 2, \begin{pmatrix}-1\\\ 0\\\ 1\end{pmatrix}, \begin{pmatrix}-1\\\ 1\\\ 0\end{pmatrix}. \\\ \text{For } \lambda_3 = 6, \begin{pmatrix}1\\\ 2\\\ 1\end{pmatrix}}$
(d) $\begin{pmatrix}1&-1&-1\\ 1&-1&0\\ 1&0&-1\end{pmatrix}$
$\Rightarrow{}\quad$ eigenvalues: $\lambda_1 = -1, \quad \lambda_2 = i, \quad \lambda_3 =-i$
For $\lambda_1 = -1$ $\Rightarrow{}\quad \begin{pmatrix}2&-1&-1\\\ 1&0&0\\\ 1&0&0\end{pmatrix}\begin{pmatrix}x_1\\\ x_2\\\ x_3\end{pmatrix} = \begin{pmatrix}0\\\ 0\\\ 0\end{pmatrix} \quad\Rightarrow{}\quad \begin{cases} 2x_1 -x_2 -x_3 = 0\\\ x_1 = 0 \end{cases}$ $\Rightarrow{}\quad \begin{cases} x_2= -x_3\\\ x_1 = 0 \end{cases}$
$\Rightarrow{}\quad$ in parametric form $x_1=0,\quad x_2=t, \quad x_3=-t$ for any $t \in R$ $\Rightarrow{}\quad$ if $t=1$, eigenvector $(0,1,-1)$
For $\lambda_2 = i$ $\Rightarrow{}\quad \begin{pmatrix}1-i&-1&-1\\\ 1&-1-i&0\\\ 1&0&-1-i\end{pmatrix}\begin{pmatrix}x_1\\\ x_2\\\ x_3\end{pmatrix} = \begin{pmatrix}0\\\ 0\\\ 0\end{pmatrix} \quad\Rightarrow{}\quad \begin{cases} x_1(1-i) -x_2 -x_3 =0\\\ x_1 -(1+i)x_2 =0\\\ x_1 -(1+i)x_3 =0 \end{cases}$ $\Rightarrow{}\quad \begin{cases} x_1 =(1+i)x_2\\\ x_2 = x_3 \end{cases}$
$\Rightarrow{}\quad$ in parametric form $x_1=(1+i)t,\quad x_2=t,\quad x_3=t$ for any $t \in R$ $\Rightarrow{}\quad$ if $t=1$, eigenvector $(1+i,1,1)$
For $\lambda_3 = -i$ $\Rightarrow{}\quad \begin{pmatrix}1+i&-1&-1\\\ 1&-1+i&0\\\ 1&0&-1+i\end{pmatrix}\begin{pmatrix}x_1\\\ x_2\\\ x_3\end{pmatrix} = \begin{pmatrix}0\\\ 0\\\ 0\end{pmatrix} \quad\Rightarrow{}\quad \begin{cases} x_1(1+i) -x_2 -x_3 =0\\\ x_1 -(1-i)x_2 =0\\\ x_1 -(1-i)x_3 =0 \end{cases}$ $\Rightarrow{}\quad \begin{cases} x_1 =(1-i)x_2\\ x_2 = x_3 \end{cases}$
$\Rightarrow{}\quad$ in parametric form $x_1=(1-i)t,\quad x_2=t,\quad x_3=t$ for any $t \in R$ $\Rightarrow{}\quad$ if $t=1$, eigenvector $(1-i,1,1)$
To summarise: $\boxed{\text{For } \lambda_1 = -1, \begin{pmatrix}0\\\ 1\\\ -1\end{pmatrix}, \\\ \text{For } \lambda_2 = i. \begin{pmatrix}1 + i \\\ 1\\\ 1\end{pmatrix}, \\\ \text{For } \lambda_3 = -i,\begin{pmatrix}1 - i \\\ 1\\\ 1\end{pmatrix}}$
Problem 3.
Let $A$ be a $2\times2$ matrix whose trace equals 2 and determinant equals -2. Find the eigenvalues of $A$. (The trace of a square matrix is the sum of the terms along it’s leading diagonal.)
$\Rightarrow{}\quad$ eigenvalues: $\boxed{\lambda_1 = 1 + \sqrt(3), \quad \lambda_2 = 1 - \sqrt(3)}$
Problem 4.
$A=\begin{pmatrix}4&-6&2\\ -1&9&-2\\ -4&12&-2\end{pmatrix}$
Given that 6 is one of the eigenvalues and its determinant is 36. Find the other eigenvalues of $A$.
$\Rightarrow{}\quad p(\lambda): \lambda^3 -11\lambda^2 +36\lambda -36 = 0$ $\Rightarrow{}\quad$ if $\lambda_1 = 6$, then $(\lambda - 6)$ is a factor of the polynomial $p(\lambda)$ then dividing the polynomial $p(\lambda)$ by $(\lambda -6)$
$\Rightarrow{}\quad \lambda^3 -11\lambda^2 +36\lambda -36 = (\lambda -6)(\lambda^2 -5\lambda + 6) = 0$
$\Rightarrow{}\quad$ eigenvalues $\boxed{\lambda_2 = 2, \quad \lambda_3 = 3}$
Problem 5.
Given that $\begin{pmatrix}-2\\ 1\\ k\end{pmatrix}$ is an eigenvector of the matrix $\begin{pmatrix}1&2&-1\\ 1&0&1\\ 4&-4&5\end{pmatrix}$ find $k$ and the corresponding eigenvalue.
$\Rightarrow{}\quad \begin{pmatrix}1-\lambda&2&-1\\\ 1&-\lambda&1\\\ 4&-4&5-\lambda\end{pmatrix}\begin{pmatrix}-2\\\ 1\\\ k\end{pmatrix} = \begin{pmatrix}0\\\ 0\\\ 0\end{pmatrix}$
$\Rightarrow{}\quad \begin{pmatrix} -2(1-\lambda) + 2 - k = 0\\\ -2 -\lambda + k = 0\\\ -8 -4 +k(5 -\lambda)=0 \end{pmatrix}$ $\Rightarrow{}\quad$ evaluating these three equations with $\boxed{\lambda_2 = 2}$
$\Rightarrow{}\quad \boxed{k = 4}$
Problem 6.
The eigenvalues of the matrix $A=\begin{pmatrix}1&1&1\\ -1&3&1\\ -1&1&3\end{pmatrix}$ are 2 and 3. Find the corresponding eigenvectors and write down a matrix which diagonalizes $A$.
$\Rightarrow{}\quad \begin{pmatrix}-1&1&1\\-1&1&1\\-1&1&1\end{pmatrix}\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix} = \begin{pmatrix}0\\0\\0\end{pmatrix}$ $\Rightarrow{}\quad -x_1 + x_2 + x_3 = 0$ $\Rightarrow{}\quad x_1 = x_2 + x_3$
$\Rightarrow{}\quad$ in parametric form $x_1=t+u, \quad x_2=t,\quad x_3=u$ for any $t,u \in R$
$\Rightarrow{}\quad$ if $t=0,\quad u=1$, eigenvector of $\lambda_1:\quad (1,0,1)^T$
$\Rightarrow{}\quad$ if $t=1,\quad u=0$, eigenvector of $\lambda_2:\quad (1,1,0)^T$
For $\lambda_3 = 3$ $\Rightarrow{}\quad \begin{pmatrix}-2&1&1\\\ -1&0&1\\\ -1&1&0\end{pmatrix}\begin{pmatrix}x_1\\\ x_2\\\ x_3\end{pmatrix} = \begin{pmatrix}0\\\ 0\\\ 0\end{pmatrix} \quad\Rightarrow{}\quad \begin{cases} -2x_1 + x_2 + x_3 = 0\\\ -x_1 + x_3 = 0\\\ -x_1 + x_2 = 0 \end{cases}$
$\Rightarrow{}\quad \begin{cases} x_1 = x_3\\\ x_1 = x_2 \end{cases}$ $\Rightarrow{}\quad$ in parametric form $x_1=t,\quad x_2=t,\quad x_3=t$ for any $t \in R$ $\Rightarrow{}\quad$ if $t=1$, eigenvector of $\lambda_3:\quad (1,1,1)^T$
$\Rightarrow{}\quad P = \begin{pmatrix}1&1&1\\\ 0&1&1\\\ 1&0&1\end{pmatrix}$ is an invertible matrix that diagonalizes $A$,
so that $P^{-1}AP = \begin{pmatrix}2&0&0\\\ 0&2&0\\\ 0&0&3\end{pmatrix}$
To summarise: For $\lambda_1 = 2$ and $\lambda_2 = 2$, eigenvectors of $\boxed{\lambda_1: (1,0,1)^T}, \boxed{\lambda_2: (1,1,0)^T}$
For $\boxed{\lambda_3 = 3, (1,1,1)^T.}$
Exam Style Questions
Problem 7.
This is the exam question from the Linear Transforms tutorial sheet with an extra part on eigenvectors and eigenvalues. The following figure shows a square in $\mathbb{R}^2$, marked with a circle and cross on its perimeter.
(a) On a single plot, sketch the result of applying the following transformation, A, to the square (including the new locations of the circle and cross).
\(A = \begin{bmatrix} 2 \ 0 \\\ 1 \ 1.5\end{bmatrix}\)
(b) On the same axes draw the spans of any eigenvectors of A and label these spans with their corresponding eigenvalues.
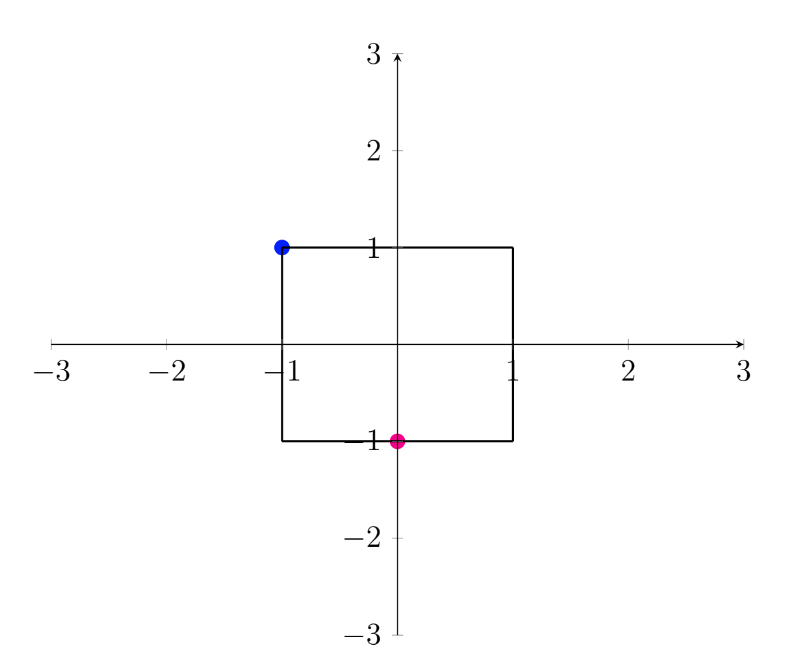
 $\boxed{\color{teal}{\lambda = 1.5, \lambda = 2}}$
$\boxed{\color{teal}{\lambda = 1.5, \lambda = 2}}$(c) Assuming the area of the initial square is 4, what is the area of this region after the transformation?
Extension Questions
Problem 8.
Let $A$ be a $3\times3$ matrix whose trace equals 5 and determinant equals -12. Given that 3 is an eigenvalue of $A$, find the other eigenvalues.
$\Rightarrow{}\quad \begin{cases} a + e +j = 5\\ a(ej - fh) - b(dj - fg) +c(dh - eg) = -12 \end{cases}\\ \Rightarrow{}\quad \begin{pmatrix}a&b&c\\d&e&f\\g&h&j\end{pmatrix} -\lambda\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix} = \begin{pmatrix}a-\lambda&b&c\\d&e-\lambda&f\\g&h&j-\lambda\end{pmatrix} = B\\ \Rightarrow{}\quad \text{det}(A) = a(ej - fh) +a(\lambda^2 -e\lambda -j\lambda) - \lambda(\lambda^2 - (e+j)\lambda +ej -fh) - \\ b(dj - fg) + bd\lambda +c(dh - eg) + cg\lambda = 0\\ \Rightarrow{}\quad -\lambda^3 + \lambda^2(a + e + j) +\lambda(bd -ae -aj -ej +fh +cg) -12 = 0\\ \Rightarrow{}\quad -\lambda^3 + 5\lambda^2 +\lambda(bd -ae -aj -ej +fh +cg) -12 = 0$
$\Rightarrow{}\quad$ for $\lambda_1 = 3,\quad bd -ae -aj -ej +fh +cg = -2$ $\Rightarrow{}\quad -\lambda^3 +5\lambda^2 -2\lambda -12 = 0 \quad\Rightarrow{}\quad (\lambda -3)(-\lambda^2 + 2\lambda +4) = 0$
$\Rightarrow{}\quad$ Eigenvalues: $\boxed{\lambda_2 = 1 + \sqrt{5},\quad \lambda_3 = 1 - \sqrt{5}}$
Problem 9.
For each of the following matrices, find an invertible matrix which diagonalizes it. (click ‘toggle answer’ to see the definition for a diagonalisable matrix)
(a) $A = \begin{pmatrix}1&3\\ 2&2\end{pmatrix}$
(b) $A = \begin{pmatrix}1&-1\\ 1&3\end{pmatrix}$
(c) $A=\begin{pmatrix}1&3&1\\ 0&5&0\\ 1&3&0\end{pmatrix}$
(d) $A = \begin{pmatrix}1&-1&-1\\ 1&-1&0\\ 1&0&-1\end{pmatrix}$
Problem 10.
Given that for a $(2\times2)$ matrix $M$, one of the eigenvalue $\lambda_1=8$ and its corresponding eigenvector $v_1=(1,1)$, it is also known that matrix $M$ changes point $(-1,2)$ to $(-2,4)$.
(a) Find matrix $M$.
$\Rightarrow{}\quad \begin{pmatrix}a&b\\\ c&d\end{pmatrix}\begin{pmatrix}1\\\ 1\end{pmatrix} = 8\begin{pmatrix}1\\\ 1\end{pmatrix}
\quad\Rightarrow{}\quad \begin{cases} a+b = 8\\\ c+d = 8 \end{cases}$
Also, from the question is is known that:
$\quad \begin{pmatrix}a&b\\\ c&d\end{pmatrix}\begin{pmatrix}-1\\\ 2\end{pmatrix} = \begin{pmatrix}-2\\\ 4\end{pmatrix}$
$\quad\Rightarrow{}\quad \begin{cases} -a+2b = -2\\\ -c+2d = 4 \end{cases}$
Solving simultaneously, we get: $\quad\Rightarrow{}\quad \begin{cases} a=6\\\ b=2\\\ c=4\\\ d=4 \end{cases}$
$\quad\Rightarrow{}\quad \boxed{M=\begin{pmatrix}6&2\\\ 4&4\end{pmatrix}}$
(b) Find $\lambda_2$ and $v_2$.
${det(M)=(\lambda-6)(\lambda-4)-8=\lambda^2-10\lambda+16=(\lambda-2)(\lambda-8)=0}$
Therefore the other eigenvalue for matrix $M$ is $\lambda=2$
For $\lambda_2 = 2, $ $\Rightarrow{}$ let $v_2= \begin{pmatrix} x \\ y \end{pmatrix} \Rightarrow{} Mv_2 =\begin{pmatrix} 6x+2y \\4x+4y\end{pmatrix}=2 \begin{pmatrix}x\\y \end{pmatrix}$ $\Rightarrow{}\quad \boxed{v_2 = \quad \begin{pmatrix} -1 \\ 2 \end{pmatrix}}$
(c) For line $l: x-y+1=0$, find $l’$ after transformed by matrix $M$.
$\Rightarrow{}\quad \begin{pmatrix}6&2\\\ 4&4\end{pmatrix}\begin{pmatrix}x\\\ y\end{pmatrix} = \begin{pmatrix}x'\\\ y'\end{pmatrix}$
$\Rightarrow{}\quad \begin{cases} x = \frac{1}{4}x'-\frac{1}{8}y'\\\ y = -\frac{1}{4}x'+\frac{3}{8}y' \end{cases}$
$\Rightarrow{}\quad x'-y'+2=0$
$\Rightarrow{}\quad l': \boxed{y=x+2}$
Answers
For Printing
Revision Questions
The questions included are optional, but here if you want some extra practice.
- Engineering Mathematics 7th edition, Stroud and Dexter : Pages 489-508, 509-518
- A-Level Exam Questions : Matricies and other integrated vector/transform questions - need to look to the past markschemes for answers
- Matrices Practice : Many practice questions, starting off with eigs but goes on to involve all previous topics.